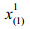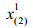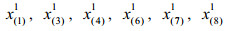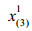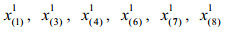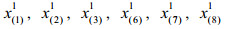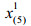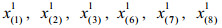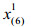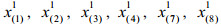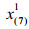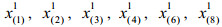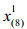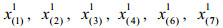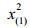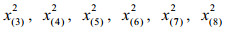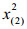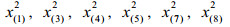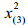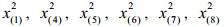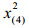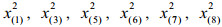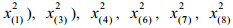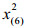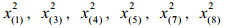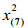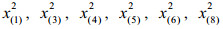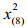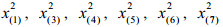2. 山西大学 中医药现代研究中心, 山西 太原 030006
2. Modern Research Center for Traditional Chinese Medicine, Shanxi University, Taiyuan 030006, China
成分数据描述的是整体中的部分,例如岩石的化学成分比例、病人血液的不同细胞类型的浓度、饮料的营养素浓度、投票选举比例等。传统的成分数据定义为含有常数和约束的非负向量[1]。由于成分数据的成分和是无意义的,因此成分数据的定义推广为仅含有相对信息的非负向量[2-3],一般用行向量x=(x1, x2, …, xD)来表示,对应的样本空间是单行空间SD。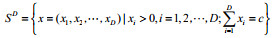
1986年,Aitchison[1]系统地研究了成分数据的统计分析,指出成分数据研究的是数据间的相对信息,而非绝对信息,提出用对数比例变换来避免常数和约束。
成分数据最早出现在地理科学中[4-5],现广泛应用于经济、化学、生物及其他学科中[6]。然而,只有很少的文献把成分数据应用在代谢组学中[7]。代谢组学[8]是对某一生物或细胞在一特定生理时期内所有低相对分子质量代谢产物同时进行定性和定量分析的一门新学科。基于核磁共振(NMR)[9]的代谢组学,谱峰面积数据获得流程:供试样品经测试,通过傅里叶变换获得NMR指纹图谱,经过定标、相位和基线校正,以合适步长进行积分,导出谱峰面积数据矩阵。通常需要对谱峰面积数据进行归一化处理,常用的归一化方法有线归一化、面归一化、模归一化[10]。无论用哪种归一化方法,归一化后数据的相对比例是不变的,都等于原始谱图中谱峰面积的相对比例,因此归一化后数据是含有相对信息的向量。由于归一化后数据是非负的,所以归一化后数据可以被考虑为是成分数据。
代谢组学领域常用的多元统计分析方法有主成分分析、聚类分析、偏最小二乘法-判别分析。通过主成分分析的得分图,可以直观看出样本的分类情况、比较同类样本的组内间距以及不同类的组间间距。偏最小二乘法-判别分析[11]常被用来寻找差异标志物,基于VIP值和S-plot图来选择差异代谢物。找出差异代谢物后,通过不同组样本间的t检验,进而得到显著的差异代谢物,即特征代谢物。跟欧氏空间上的普通数据相比,成分数据所属的单行空间上有相应的运算和度量,因此传统的统计分析方法不能直接应用于成分数据。考虑到成分数据特有的度量向量空间结构,本文基于成分数据分析研究代谢组学中常常需要涉及的问题:(1)样本初始分布状态,即各组样本的相似性;(2)在确定样本的分类后,需要对分组贡献大的关键差异成分进行表征;(3)建立的分类模型有望对新的未知样本进行预测,即进行判别分析。
本文对成分数据的基本知识进行简要介绍,提出基于核磁共振代谢组学的成分数据分析方法,并以黄芪质量评价为例对该方法进行验证。
1 成分数据的基本知识成分数据的基本运算、度量及其描述性统计的定义[1-3]如下。对于任意的成分数据x∈SD, y∈SD和实数 
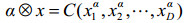
成分数据x∈SD和y∈SD的Aitchison距离定义为da(x, y)。
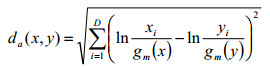
|
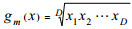
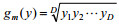
给定成分数据集:

|
(1) |
其中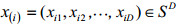
公式(1)中的成分数据集X的样本中心定义为:
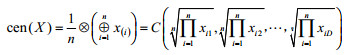
|
公式(1)中的成分数据集X的离差可以用方差矩阵来描述,定义为:
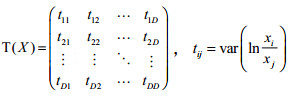
|
公式(1)中的成分数据集X的总离差的测量是总方差,定义为:
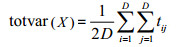
|
给定成分数据x∈SD,子成分定义为xS=C (xS),其中S是D×S(D≤S)的选择矩阵,该矩阵中每列有一个元素为1,每行最多有一个元素为1,其余元素为0。同理,对于公式(1)中的成分数据集X,子成分数据集XS定义为:
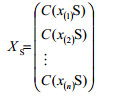
|
代谢组学一般研究多组样本,假定有G组样本,则所有样本的谱峰面积归一化后数据可以用n×D的数据集X表示。
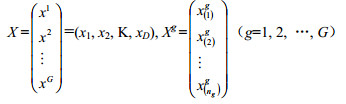
|
其中X的每行表示每个样本的谱峰面积归一化后数据,每列表示某个代谢物,xj (j=1, 2, …, D)为第j个变量,Xg (g=1, 2, …, G)代表第g组样本数据集,ng为第g组的样本个数,且n1+n2+…+ng=n,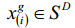
对于同一组的样本数据集Xg (g=1, 2, …, G),如果用图形来表示样本点,样本点越密集,即样本点离数据集中心的距离越小,则该样本数据集的均一性越好。因此,所有样本点与中心的Aitchison距离的平方和的平均值可以当作是样本数据集的均一性评价指标,即
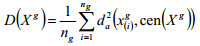
|
(2) |
如果D(Xg)越小,则该组数据集的均一性越好。
2.2 筛选特征代谢物方差用来衡量数据的波动程度,所以方差大的变量有可能是不同组的差异代谢物。差异代谢物选取方法的基本思想是从方差小的那些变量开始依次剔除,直到上一步和下一步的总方差的相对误差大于给定的临界值时停止剔除变量。不失一般性,假定var (x1)≥var (x2)≥…≥var (xD),计算步骤如下:
(1)令k=0,定义X0=X为原始的样本数据集,计算totvar (X0)。
(2)剔除变量xD-k。记Xk+1=(x1, x2, …, xD-k-1)为剔除变量xD-k, xD-k+1, …, xD后的子成分样本数据集,计算totvar (Xk+1)。根据子成分一致性原则[1],有totvar (Xk)≥totvar (Xk+1)。
(3)当上一步和下一步总方差的相对误差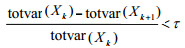
通过以上迭代过程,Xk为最终选取的子成分数据集,x1, x2, …, xD-k为最终选取的差异变量。接下来用t检验对差异变量的任意2组样本进行显著性检验,当有P<0.05时,该变量即为显著的差异代谢物,即特征代谢物。
2.3 新样本进行判别分析用基于Aitchison距离的k近邻法来验证寻找的特征代谢物对新样本的分类能力,基本思路:根据Aitchison距离找到离预测实例最近的k个样本点,基于多数表决的规则,这k个样本点的多数属于某个类,则预测实例就属于这个类。
3 黄芪质量评价的实例分析研究甘肃黄芪和山西黄芪的化学成分,数据来源于文献报道[12],分别为8批甘肃移栽速生芪和8批山西传统野生黄芪。采用传统水煎,冷冻干燥后,用氘代重水溶解进行1H-NMR测试,所得自由衰减信号导入MestReNova软件(version 8.0.1,Mestrelab Research,Santiago de Compostella,Spain),以δ 0.04积分段对化学位移区间0.78~9.22进行分段积分,其中δ 4.66~5.06残留水峰不进行积分,导出数据矩阵进行统计分析。样本X数据集为:
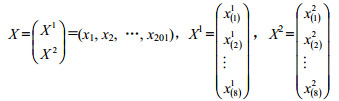
|
其中X1代表甘肃黄芪,X2代表山西黄芪,xj (j=1, 2, …, 201)为第j个变量。根据公式(2)计算得出D(X1)=79.360 0,D(X2)=83.806 5,因此甘肃黄芪均一性相比山西的黄芪较好。实际上,甘肃黄芪作为市场上主流商品黄芪,一般生长2年,且加工后几乎拥有相同的直径和长度,因而各批所含化学成分的量相对均匀,而山西黄芪作为传统野生黄芪,据传统经验一般生长5年以上,但具体年限不详,因而本实验收集的不同批山西黄芪的均一性相对较差。根据“2.2”项方法选取特征代谢物,结果见表 1,该方法除找到与文献报道[12]一样的特征代谢物外,还找到特征代谢物异亮氨酸、缬氨酸、精氨酸、谷氨酰胺、β-木糖、α-葡萄糖、苯丙氨酸。根据找到的特征代谢物对给定的样本进行判别分析,采用留一交叉法验证,每次选取一个样本当作预测样本,其余样本当作训练样本,用基于Aitchison距离的k近邻法来验证分类的准确性,结果见表 2。从表 2可以看出,对于每个给定的样本都分类正确。基于文献报道[12]找到的特征代谢物,运用同样的判别分析方法对给定的样本进行判别分析,分类准确度达100%。
|
|
表 1 特征代谢物对应的的变量、化学位移和化合物名称 Table 1 Corresponding variable, chemical shift, and compound of characteristic metabolites |
|
|
表 2 基于Aitchison距离的k近邻法判别分析结果 Table 2 Results of discriminate analysis by k nearest neighbor method based on Aitchison distance |
4 结语
迄今为止,对于代谢组学的数据分析有很多方法,但鲜有学者将代谢组学数据考虑为成分数据。本文基于成分数据的知识来研究代谢组学常常关心的问题,实例分析结果表明样本均一性评价与实际情况相符、筛选的特征代谢物与文献报道[12]一致、判别分析的准确性高。在之后的研究中,希望基于成分数据的回归分析或相关分析来研究若干因变量与自变量的相互依赖关系,例如植物代谢组学研究中,环境因素(气温、湿度、日照等)与影响不同产地植物分类的差异代谢物之间的相互依赖关系,或临床生化指标与体液代谢组学的潜在生物标志物之间的相互依赖关系。
| [1] | Aitchison J. The Statistical Analysis of Compositional Data[M]. London: Chapman & Hall, 1986 . |
| [2] | Pawlowsky-Glahn V, Buccianti A. Compositional Data Analysis:Theory and Applications[M]. Chichester: John Wiley & Sons Ltd, 2011 . |
| [3] | Pawlowsky-Glahn V, Egozcue J J, Tolosana-Delgado R. Modeling and Analysis of Compositional Data[M]. Chichester: John Wiley & Sons Ltd, 2015 . |
| [4] | Sun X L, Wu Y J, Wang H L, et al. Mapping soil particle size fractions using compositional kriging, cokriging and additive log-ratio cokriging in two case studies[J]. Math Geosci , 2014, 46 (4) :429–443. DOI:10.1007/s11004-013-9512-z |
| [5] | Tolosana-Delgado R, Von Eynatten H. Simplifying compositional multiple regression:Application to grain size controls on sediment geochemistry[J]. Comput Geosci , 2010, 36 (5) :577–589. DOI:10.1016/j.cageo.2009.02.012 |
| [6] | Lin W, Shi P, Feng R, et al. Variable selection in regression with compositional covariates[J]. Biometrika , 2014, 101 (4) :785–797. DOI:10.1093/biomet/asu031 |
| [7] | Kalivodová A, Hron K, Filzmoser P, et al. PLS-DA for compositional data with application to metabolomics[J]. J Chemometr , 2015, 29 (1) :21–28. DOI:10.1002/cem.2657 |
| [8] | Nicholson J K, Connelly J, Lindon J C, et al. Metabonomics:a platform for studying drug toxicity and gene function[J]. Nat Rev Drug Discov , 2002, 1 (2) :153–161. DOI:10.1038/nrd728 |
| [9] | Kim H K, Choi Y H, Verpoorte R. NMR-based metabolomic analysis of plants[J]. Nat Prot , 2010, 5 (3) :536–549. DOI:10.1038/nprot.2009.237 |
| [10] | 温锦波, 杨叔禹, 肖娴, 等. 基于核磁共振的代谢组学数据预处理[J]. 厦门大学学报:自然科学版 , 2007, 46 (6) :783–787. |
| [11] | Xiong A Z, Yang L, Ji L L, et al. UPLC-MS based metabolomics study on Senecio scandens and S.vulgaris:an approach for the differentiation of two Senecio herbs with similar morphology but different toxicity[J]. Metabolomics , 2011, 8 (4) :614–623. |
| [12] | Li A P, Li Z Y, Sun H F, et al. Comparison of two different Astragali Radix by a 1H-NMR-based metabolomic approach[J]. J Proteome Res , 2015, 14 (5) :2005–2016. DOI:10.1021/pr501167u |
 2016, Vol. 47
2016, Vol. 47